研究紹介
産業数理統計研究部門では、諸科学・産業における統計の問題を、数学的手法を提案することによって対処し、様々な社会課題を解決することを目指しています。応用分野として、エネルギー、材料科学、地球科学等の自然科学のみならず、公的統計、心理統計等の社会科学にも及んでいます。いくつかの手法はソフトウェアパッケージとして実装されており、他分野の研究や実務で使われています。具体的な研究内容としては、スパース推定やロバスト推定、小地域推定等の数理統計・機械学習の理論的研究、および情報学、幾何学、代数学等との分野の垣根を超えた融合研究を行っています。
エネルギービッグデータ解析手法の開発
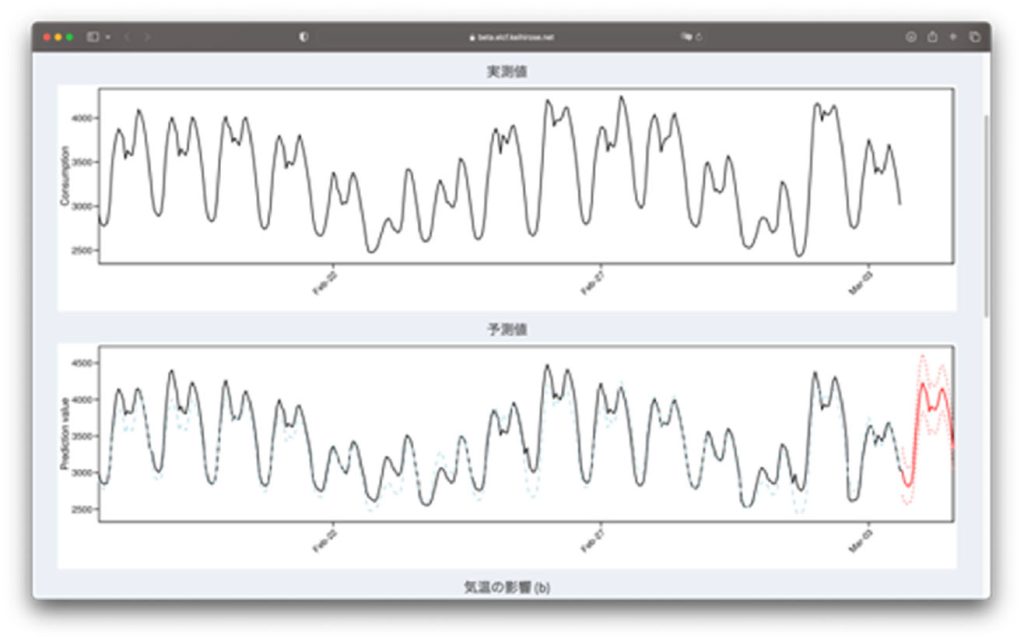
近年はウクライナ情勢等で我が国におけるエネルギーの状況が刻々と変わっており、電気代高騰等エネルギー問題は身近なものとなっております。そのような中、太陽光発電や洋上風力等、再生可能エネルギーを用いることが考えられますが、発電が不安定であるという問題があります。そのため、発電量、電力需要、電力価格等を精度良く予測することが求められます。そこで、一般化Lasso等の高度な手法を用いた高精度な予測、リスクマネジメントに役立つ予測区間の構築を行っています。さらに、この予測アルゴリズムを手軽に使えるソフトウェアも作成しています。
関連するプロジェクト:https://coi.kyushu-u.ac.jp , https://recow.kyushu-u.ac.jp
材料データ解析手法の開発
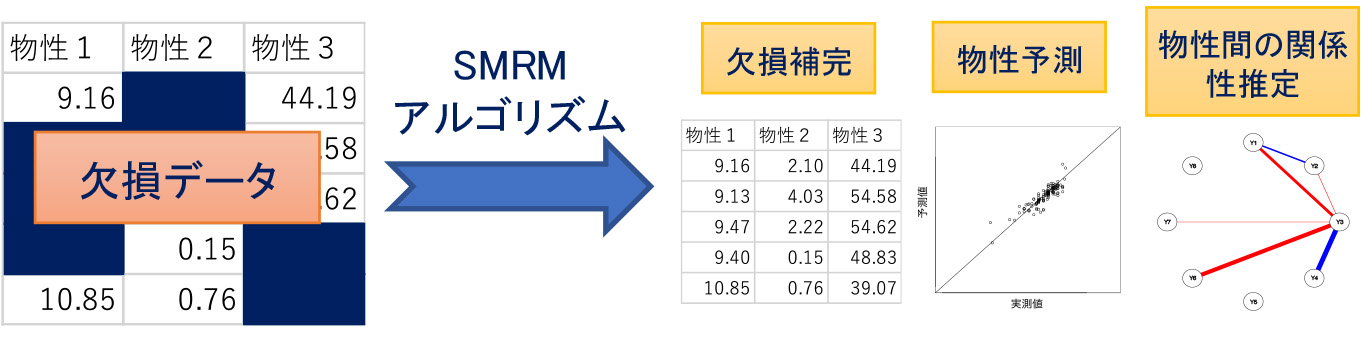
材料開発は、従来は様々な条件下での実験結果から行われるものでしたが、近年はデータサイエンスによって行われるようになりつつあります。接着強度等の物性を予測するためには、統計モデルの構築が必要となります。とくに、企業間のデータ共有が難しい場合は、十分なサンプルサイズが得られないことが多いです。さらには、データに欠測が生じることもあります。そこで、欠測がある場合でも、少ないサンプルから精度良く予測する統計解析手法を開発しています。また、実験間にはばらつきが生じますので、物性のみならず、そのばらつきをも推定する手法も開発しております。現在、未来社会創造事業のCREAプロジェクトで本研究とその社会実装を推進しています。
関連するプロジェクト:https://crea.kyushu-u.ac.jp/group/廣瀬-慧-グループ/
位相的データ解析と機械学習
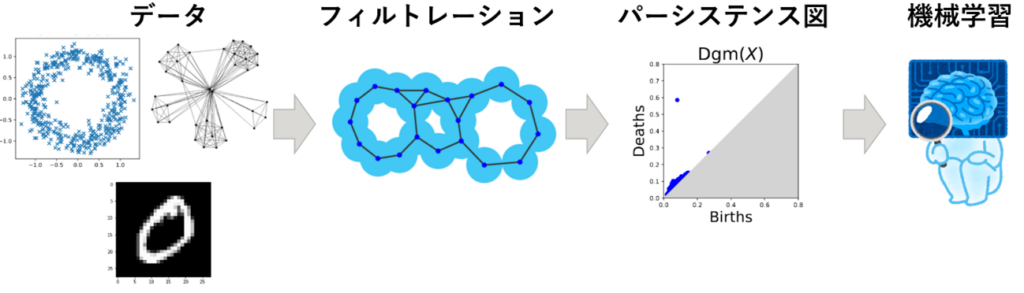
位相的データ解析は、データの「大まかな形」を特徴量として抽出する、2000年ごろに開発された比較的新しい手法です。現在では、物質科学のデータや医療データの解析に適用されるようになってきています。
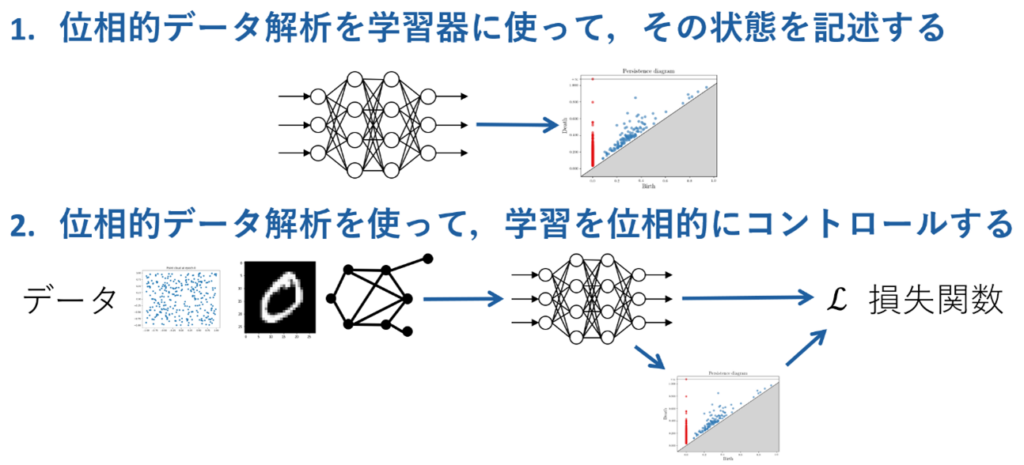
近年は、位相的データ解析は機械学習手法と組み合わされて発展してきており、「大まかな形」をあらわす特徴量をニューラルネットワークに入力する際の良い変換方法や、そのような特徴量抽出をニューラルネットワークで学習するといった手法を開発してきました。また、位相的データ解析の手法をデータに使うのではなく、ニューラルネットワークなどの学習器そのものに使うことで、学習器の状態を把握したり、位相的に学習をコントロールしたりという研究も行っています。これらの研究は、富士通研究所とフランスの研究機関Inriaと共同で推進してきました。
小区分別推定手法の理論研究と応用への適用可能性の吟味
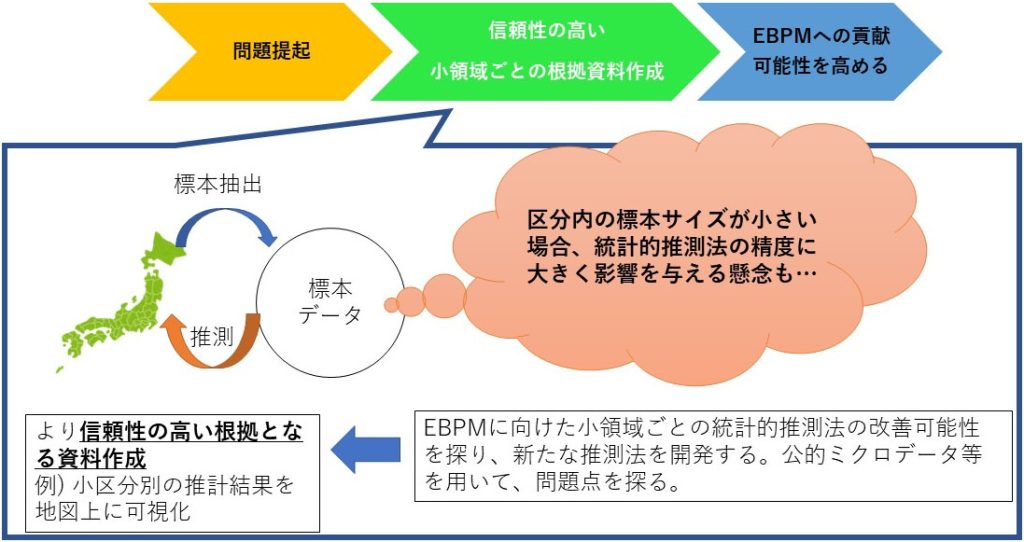
小区分別に推定することは、丁寧な実態把握をするうえでメリットがあります。例えば、日本全国の平均値ではなく、もっと細かな区分ごとの特性値を把握したい場合を想像して下さい。しかしその一方で、各区分内の標本サイズが小さくなり、各区分内の情報のみに基づく推定手法の信頼性が低くなってしまうかもしれません。対して、混合効果モデル、経験ベイズ法、ベイズ法の枠組みを用いると、その推定の不安定さを軽減できる可能性もあります。しかしながら、既存の手法には、理論面では気にされていなかったような実用面での問題も生じ得ます。現在は、それら両面を意識した新たな推定手法の開発可能性とその理論保証に取り組んでいます。
さらに、そのような推定手法の応用分野への適用にも興味を持っています。現在は、我が国におけるEBPM(Evidence Based Policy Making)への貢献可能性を追求しており、公的ミクロデータ(https://www.e-stat.go.jp/microdata/)を利用して貧困実態把握や観光統計に関する研究プロジェクトに携わっています。また、統計的開示制御の理論研究にも最近取り組んでいます。
外部連携など
- 九州大学 数理・データサイエンス教育研究センター 協力教員
https://mdsc.kyushu-u.ac.jp/
教材提供 - 福岡県データ利活用アドバイザー
特殊なデータに強い分析手法の開発・応用(ロバストネス)
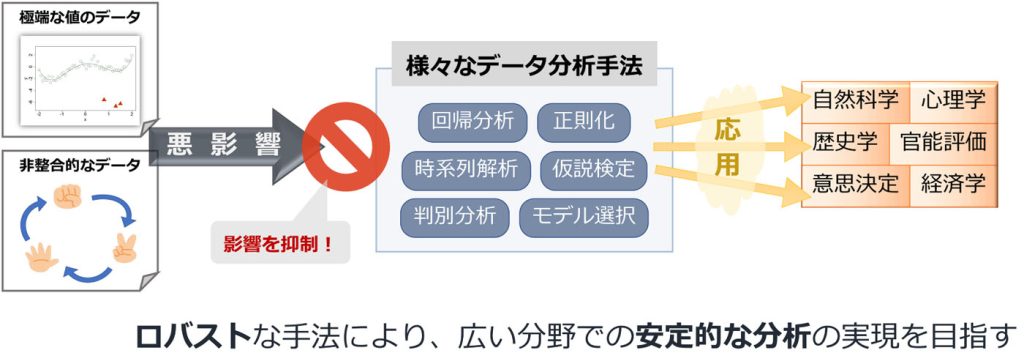
企業戦略を考えるにあたって、商品やサービスに関する顧客からのアンケートを適切に分析することは重要です。しかし、人間の感じ方は機械のように整合的とは限らず、多数派と異なった極端な回答や、「AよりもBが好ましい」「BよりもCが好ましい」と答えた人が「CよりもAが好ましい」と答えるというような矛盾した回答は、少数とはいえ充分に有り得ます。そういった特殊な回答が混ざっていると、一般的な分析手法はそれに引っ張られて妥当性のない結論を導いてしまいがちです。そこで、非整合的なデータや極端なデータが分析対象に含まれていてもいなくても、全体の情報を安定的に分析できる「ロバスト」な統計的手法の開発を行っています。また、これまで因果関係を記述するモデルや人間の選好を表現するモデル等においてロバストな手法を導入し、従来手法よりも安定的な分析に取り組んできました。
統計モデルの選択に関する研究(モデル選択)
現象を記述するための最適な統計モデルを探る選択問題には、文理を問わず幅広い分野で直面します。よく用いられる有名なモデル選択手法には情報量規準AICやBICがあり、またLasso等のスパース正則化を応用した選択も有用です。なお、モデル選択手法にはそれぞれ違った特長や弱点が存在し、いつ何時も特定の一手法を使い続けるのが最善である、とは限りません。そのため、分析するデータの精査と理論的性質の究明により、それぞれの分野に応じた適切なモデルを選ぶ適切な手法について検討することには大きな意義があります。例えばこれまでには、味や食感に対する感じ方の傾向とそれに影響を与える特性について情報量規準を用いて検討する研究や、人が意思や行動を決める基準を適切に記述するモデルを外れ値に対するロバスト性に優れた手法で選択する研究等を行ってきました。選択手法の良さを究明し、それぞれの問題に応じた適切なモデルを導くことを目指しています。
因子分析の理論研究
因子分析は、1904年にCharles Spearman氏によって提案された、歴史の古い統計解析手法です。因子分析は、もともと心理学や社会科学で取得されるアンケートやテストのデータに用いられてきましたが、近年は、高次元データの次元圧縮の手法として、経済、生命科学、材料科学など、様々な分野で使われています。数学的には、状態空間モデルやニューラルネットワークの特殊な場合とみなすことができ、あらゆる統計モデルの基礎をなしています。そのため、因子分析の徹底的な基礎研究は、統計学や機械学習の発展につながると考えられます。
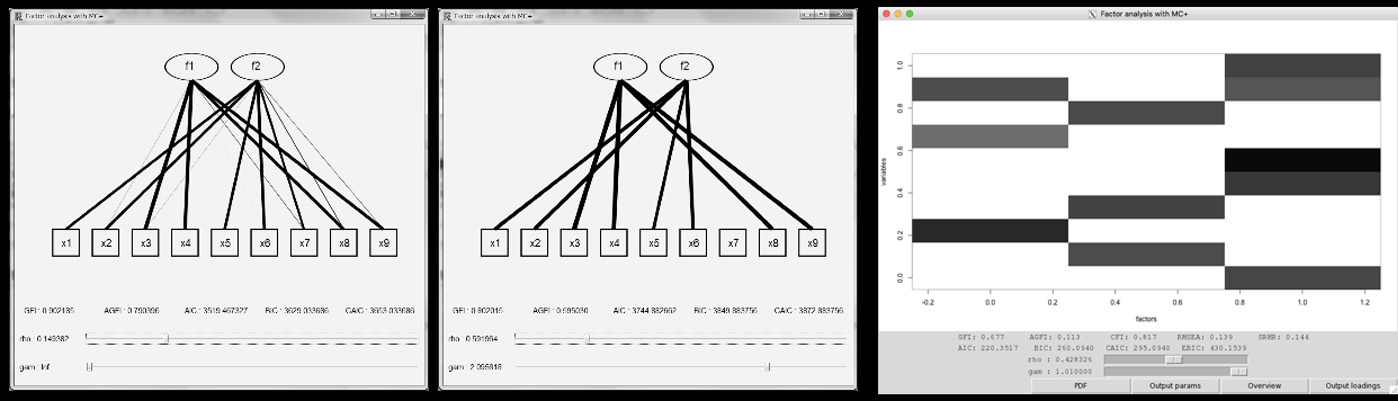
因子分析では、因子の解釈のため、これまで約三四半世紀もの間、因子回転が広く使われてきました。この方法をホモトピー法に基づいて解析すると、実は、因子回転の一般化として正則化法が挙げられることが理論的に示されることがわかりました。このことは、因子分析におけるスパース推定の理論的裏付けとなります。そこで、これまで様々なスパース正則化法に基づくスパース因子分析を提案し、さらに誰でも実行できるよう、Rパッケージfancを作成しました。このパッケージは、パラメータの推定値の計算とその可視化を行うことができ、統計学者のみならず、他分野の研究者にも実証研究で使われつつあります。
最近は、九大数理の深作亮也先生、加葉田雄太朗先生(長崎大)、寺本圭佑先生(広島大)との共同研究を通じて、因子分析の最尤解を代数的に解き、幾何的な構造を理解するというという、極めてチャレンジングな研究を推進しています。
ベイズ推定による計測と数理モデリングの橋渡し
古くは17世紀に発見されたケプラーの法則が象徴するように、単純な数式を用いて計測データを表す数理モデリングは様々な物理現象に対する理解を深めてきました。しかし、扱う現象が複雑になり、高度な計測技術を駆使する現代科学では理解が困難な計測データが顕在化しています。我々は計測データに根ざしたモデリング原理の確立により、あらゆる現象を曖昧さなく理解するための指針を打ち出す研究に挑戦しています。特にベイズ推定という統計的手法の数理を探求するとともに、固体物理学、ソフトマター物理学、プラズマ物理学などの研究者との異分野協働による実証研究を推進しています。
|
|
関連するプロジェクト:
・計測・解析プロセス革新のための基盤の構築 / 計測データに根ざしたモデリング原理の革新
プレスリリース:
・計測データの量や質に対するベイズ推定のスケーリング則を解明
・ベイズ推定を用いた新たな電子構造の解析法を開発
・ベイズ推定を用いた速度分布関数の解析法を開発
